🧑🏻‍💻 排序

记录了 C++ 中几种排序方法的实现。作笔记用。

发表于 2024/09/17 更新于 2025/01/10

作者尘心

次浏览 13 分钟阅读

🧑🏻‍💻 排序

Characteristics of sorting algorithms:

In-place: a sorting algorithm is in-place if $O(1)$ extra space is needed beyond input.
Stability: a sorting algorithm is stable if numbers with the same value appear in the output array in the same order as they do in the input array.

Procedure 𝐈𝐧𝐬𝐞𝐫𝐭𝐢𝐨𝐧-𝐒𝐨𝐫𝐭¹

In: An array $A$ of $n$ integers.
Out: A permutation of that array $A$ that is sorted (monotonic).

for $i := 2$ to $A.length$
$key := A[i]$
// Insert $A[i]$ into the sorted subarray $A[1 : i - 1]$
$j := i - 1$
while $j > 0$ and $A[j] > key$
$A[j + 1] := A[j]$
$j := j - 1$
$A[j + 1] := key$
return $A$

One possible implementation with C++:

  
int main()
{
    int arr[100], len;
    cin >> len;
    for (int t = 0; t < len; t++)
      cin >> arr[t];
    for (int i = 1; i < len; i++)
    {
      int key = arr[i];               // 把要比较的牌从手牌里单独抽出来
      int j = i - 1;
      while (j > 0 && arr[j] > key)   // 将此牌与前面的牌比较大小
      {
        arr[j + 1] = arr[j];          // 把前面的大牌依次往后挪，空出位置
        j--;
      }
      arr[j + 1] = key;               // 把此牌插入合适的位置
    }
    for (int t = 0; t < len; t++)
      cout << arr[t] << " ";
    return 0;
}

Procedure 𝐌𝐞𝐫𝐠𝐞-𝐒𝐨𝐫𝐭

In: An array $A$ of $n$ integers.
Out: A permutation of that array $A$ that is sorted (monotonic).

MergeSort($A[1…n]$):
if $n = 1$
$sol[1…n] = [1…n]$
else
$solLeft[1…(n/2)] := MergeSort(A[1…(n/2)])$
$solRight[1…(n/2)] := MergeSort(A[(n/2 + 1)…n])$
$sol[1…n] := Merge(solLeft[1…(n/2)], solRight[1…(n/2)])$
return $sol[1…n]$

Merge($A[1…n], B[1…m]$):
$Aindex := 1, Bindex := 1, Result := [ ]$
// Scan $A$ and $B$ from left to right,
// Append the currently smallest to the result array.
while $Aindex \leq A.length$ and $Bindex \leq B.length$
if $A[Aindex] \leq B[Aindex]$
$Result.AddLast(A[Aindex])$
$Aindex := Aindex + 1$
else
$Result.AddLast(B[Bindex])$
$Bindex := Bindex + 1$

// Copy the remaining elements of A and B
while $Aindex \leq A.length$
$Result.AddLast(A[Aindex])$
$Aindex := Aindex + 1$
while $Bindex \leq B.length$
$Result.AddLast(B[Bindex])$
$Bindex := Bindex + 1$
return $Result$

One possible implementation with C++:

  
void merge(int a[], int result[], int left, int mid, int right)
{
    int i = left, j = mid + 1, k = left;

    // 按大小顺序依次添加到 result 数组中
    while (i <= mid && j <= right)
    {
    if (a[i] <= a[j])
        result[k++] = a[i++];
    else
        result[k++] = a[j++];
    }

    // 处理剩余的数
    while (i <= mid)
        result[k++] = a[i++];
    while (j <= right)
        result[k++] = a[j++];

    for (i = left; i <= right; i++)
        a[i] = result[i];
}

void merge_sort(int a[], int result[], int left, int right)
{
    if (left < right)
    {
        int mid = (left + right) / 2;
        merge_sort(a, result, left, mid);
        merge_sort(a, result, mid + 1, right);
        merge(a, result, left, mid, right);
    }
}

Procedure 𝐇𝐞𝐚𝐩-𝐒𝐨𝐫𝐭

Keep a copy of the root item
Remove last item and put it to root
Maintain heap property
Return the copy of the root item

One possible implementation with C++:

  
#include <bits/stdc++.h>
using namespace std;

// maintain heap property
void heapify(int arr[], int n, int i) 
{
    int left = 2 * i + 1;
    int right = 2 * i + 2;
    int largest = i;

    if (left < n && arr[left] > arr[largest])
        largest = left;
    if (right < n && arr[right] > arr[largest]) 
        largest = right;
    if (largest != i) 
    {
        swap(arr[i], arr[largest]);
        heapify(arr, n, largest);
    }
}

void heapSort(int arr[], int n) 
{
    // build max heap   
    for (int i = n / 2 - 1; i >= 0; i--) 
        heapify(arr, n, i);

    // swap the root item with the last item,
    // then heapify the remaining items
    for (int i = n - 1; i >= 0; i--) 
    {
        swap(arr[0], arr[i]);
        heapify(arr, i, 0);
    }
}

Procedure 𝐒𝐞𝐥𝐞𝐜𝐭𝐢𝐨𝐧-𝐒𝐨𝐫𝐭

Basic idea: pick out minimum element from input, then recursively sort remaining elements, and finally concatenate the minimum element with sorted remaining elements.

In: An array $A$ of $n$ integers.
Out: A permutation of that array $A$ that is sorted (monotonic).

SelectionSort($A$):
for $i := 1$ to $A.length$
$minIdx := i$
for $j := i + 1$ to $A.length$
if $A[j] < A[minIdx]$
$minIdx := j$
$Swap(i, minIdx)$

One possible implementation with C++:

  
void SelectSort(int* arr, int n)
{
    // 保存参与单趟排序的第一个数和最后一个数的下标
    int begin = 0, end = n - 1;
    while (begin < end)
    {
        int maxIndex = begin; // 保存最大值的下标
        int minIndex = begin; // 保存最小值的下标

        // 找出最大值和最小值对应的下标
        for (int i = begin; i <= end; ++i)
        {
            if (arr[i] < arr[minIndex])
                minIndex = i;
            if (arr[i] > arr[maxIndex])
                maxIndex = i;
        }

        // 最小值放在序列开头
        swap(&arr[minIndex], &arr[begin]); 

        // 如果最大值原本在 begin 位置，即 maxIndex == begin，
        // 那么上面的操作会将最大值换到下标为 minIndex 处，
        // 此时 maxIndex 不再是最大值的下标，而是最小值的。
        // 为了防止以上情况发生，我们需要更新一下 maxIndex。
        if (begin == maxIndex)
            maxIndex = minIndex;
        
        // 最大值放在序列结尾
        swap(&arr[maxIndex], &arr[end]); 

        ++begin;
        --end;
    }
}

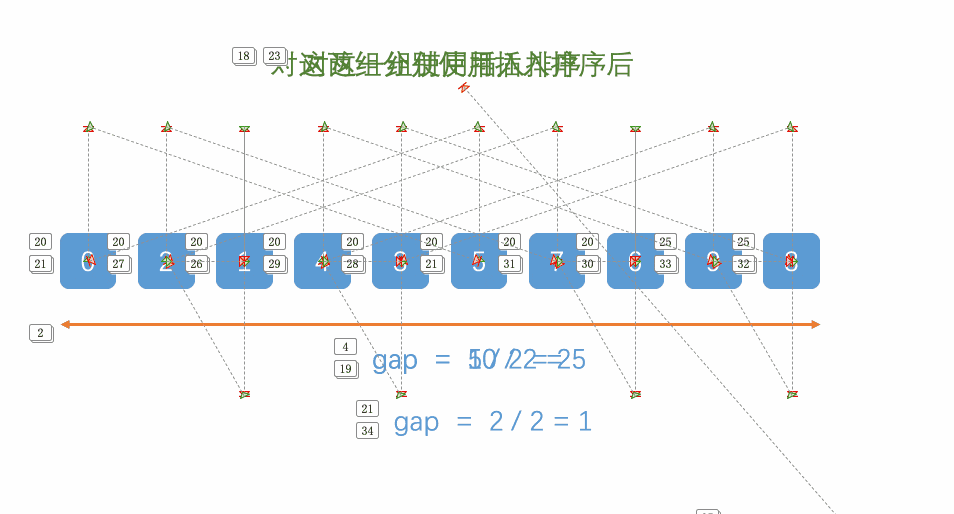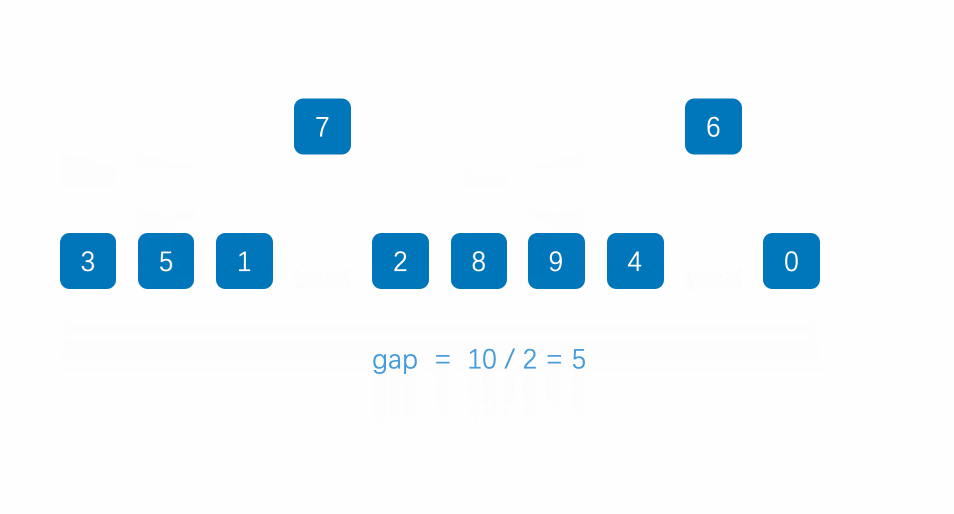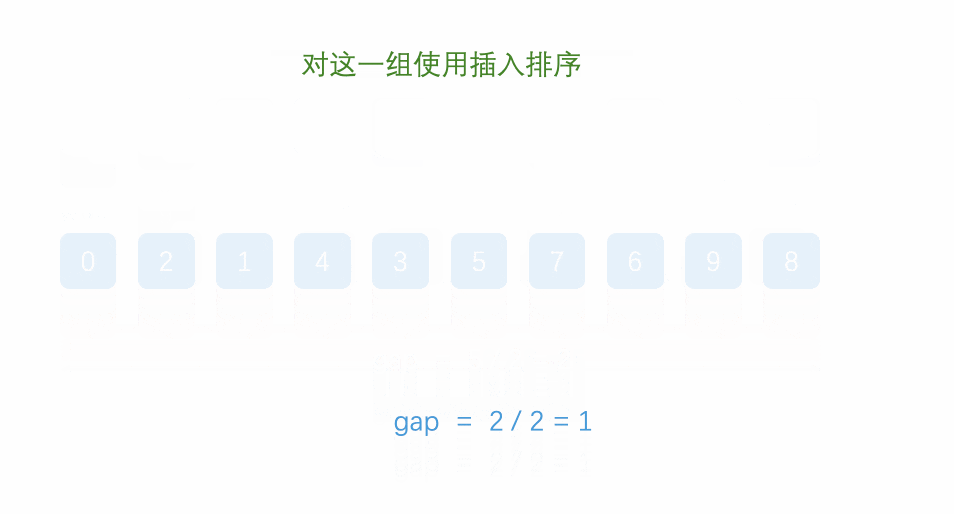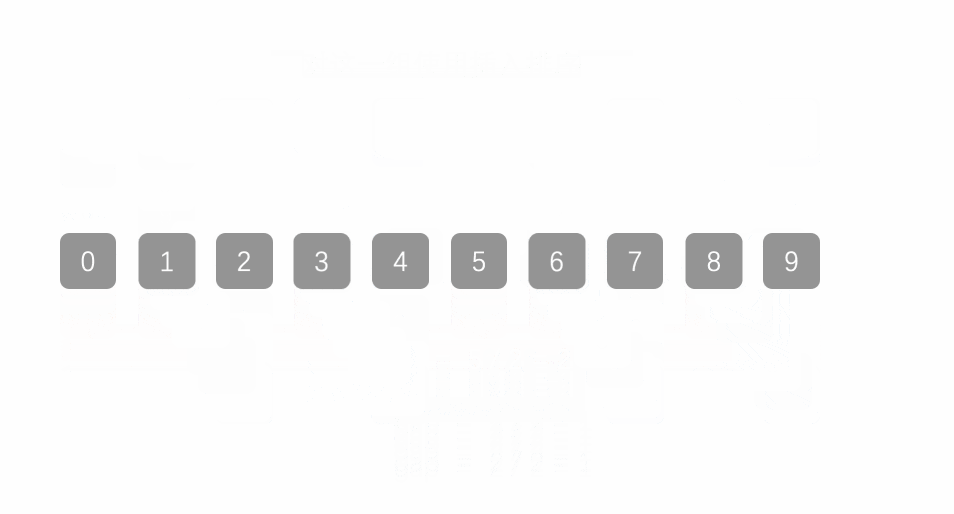
Procedure 𝐒𝐡𝐞𝐥𝐥-𝐒𝐨𝐫𝐭

One possible implementation with C++:

  
#include <bits/stdc++.h>
using namespace std;

void ShellSort(vector<int> &nums)
{
    int size = nums.size();
    for (int gap = size / 2; gap > 0; gap /= 2)
    {
        // 使用插入排序对当前间隔进行排序
        for (int i = gap; i < size; i++)
        {
            int key = nums[i];
            int j = i;
            while (j >= gap && nums[j - gap] > key)
            {
                nums[j] = nums[j - gap];
                j -= gap;
            }
            nums[j] = key;
        }
    }
}

Procedure 𝐁𝐮𝐛𝐛𝐥𝐞-𝐒𝐨𝐫𝐭

Basic idea: repeatedly step through the array, compare adjacent pairs and swaps them if they are in the wrong order. Thus, larger elements “bubble” to the “top”.

In: An array $A$ of $n$ integers.
Out: A permutation of that array $A$ that is sorted (monotonic).

BubbleSort($A$):
for $i := A.length$ down to $2$
for $j := 1$ to $i - 1$
if $A[j] > A[j + 1]$
$Swap(A[j], A[j + 1])$

One possible implementation with C++:

  
void BubbleSort(int arr[], int len) 
{
        int i, j;
        for (i = 0; i < len - 1; i++)
        {
            for (j = 0; j < len - 1 - i; j++)
            {
                if (arr[j] > arr[j + 1])
                {
                    swap(arr[j], arr[j + 1]);
                }
            }
        }
}

Procedure 𝐐𝐮𝐢𝐜𝐤-𝐒𝐨𝐫𝐭

Basic idea: Given an array $A$ of $n$ items.

Choose one item $x$ in $A$ as the pivot.
Use the pivot to partition the input into $B$ and $C$, so that items in $B$ are $\leq x$, and items in $C$ are $> x$.
Recursively sort $B$ and $C$.
Output $⟨B, x, C⟩$.

In: An array $A$ of $n$ integers.
Out: A permutation of that array $A$ that is sorted (monotonic).

QuickSortAbs($A$):
$x := GetPivot(A)$
$<B, C> := Partition(A, x)$
$QuickSortAbs(B)$
$QuickSortAbs(C)$
return $Concatenate(B, x, C)$

One possible implementation with C++:

  
#include <bits/stdc++.h>
using namespace std;

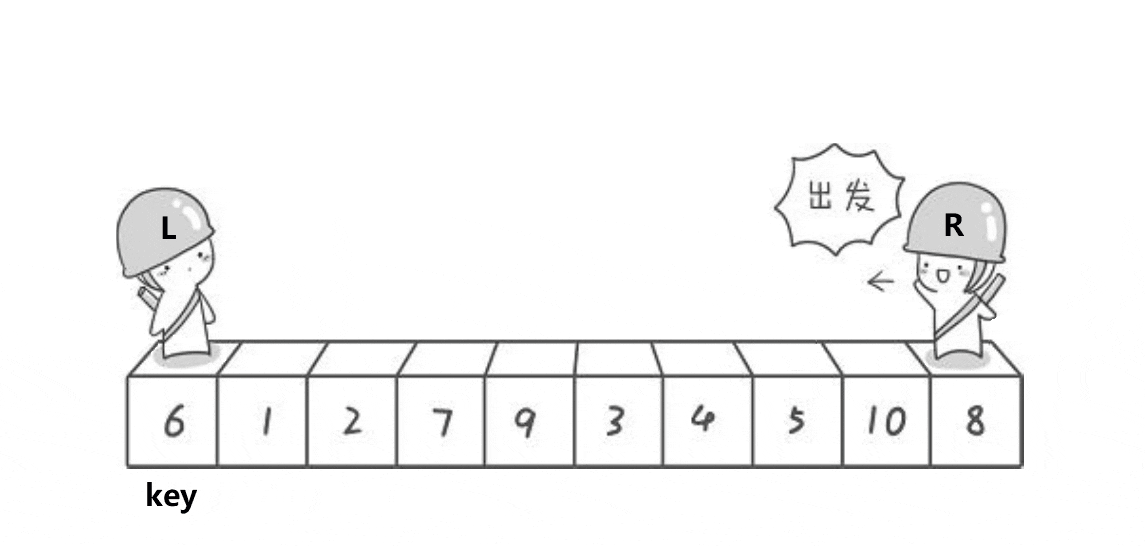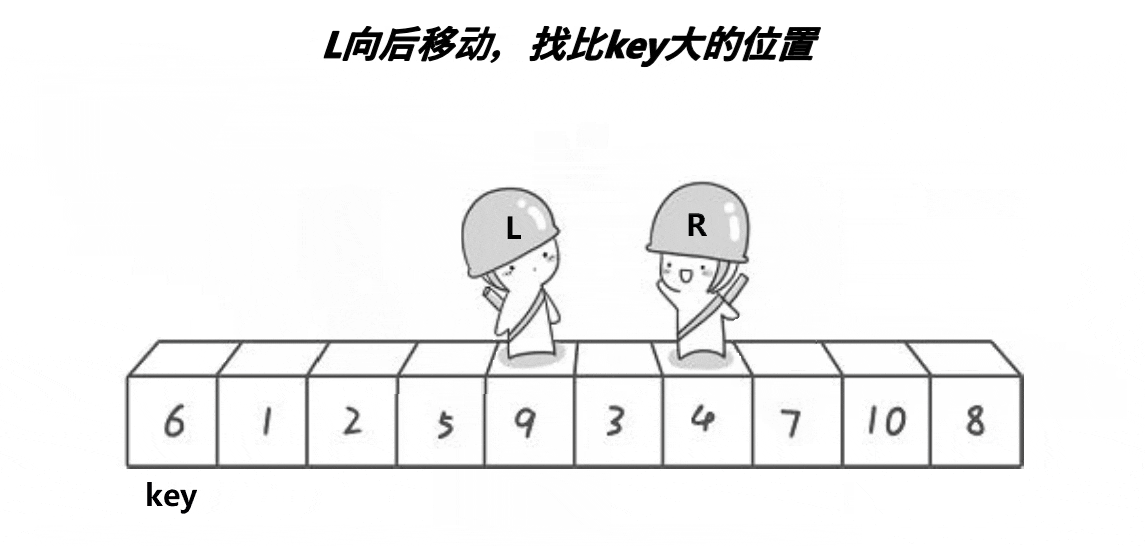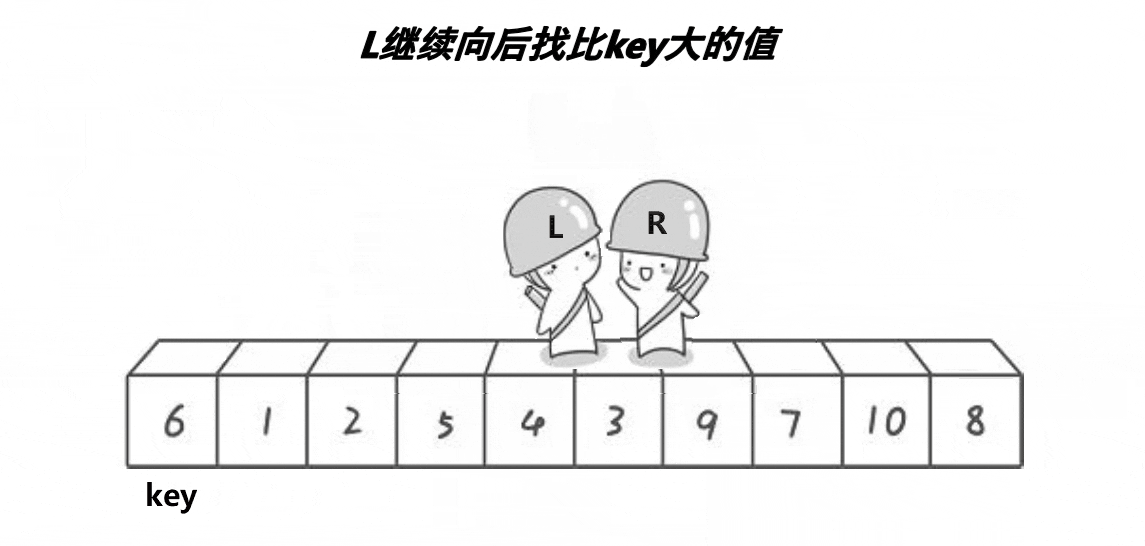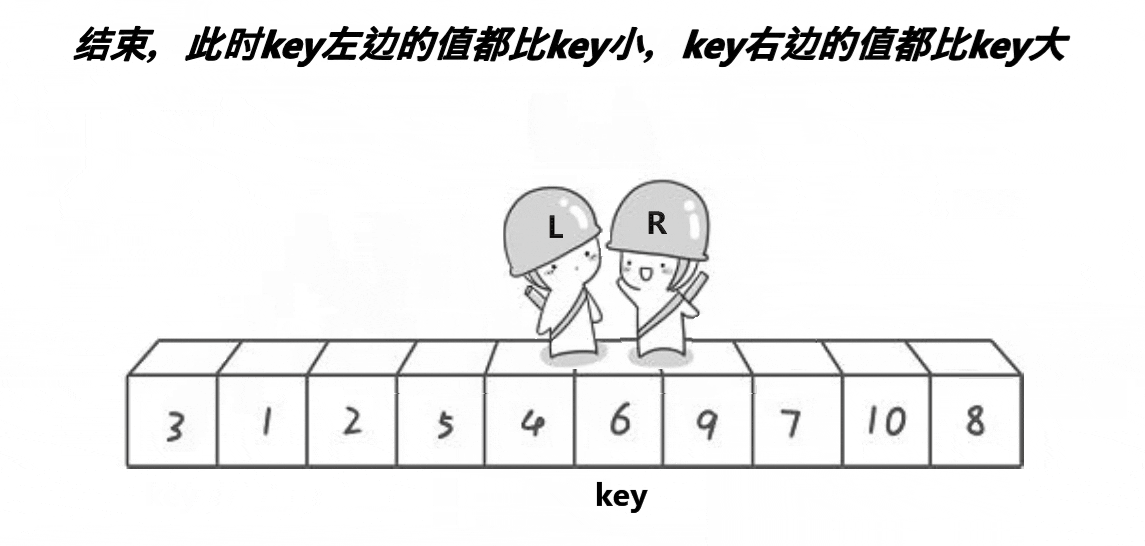
// 选定一个 pivot 并将 left 到 right 之间的元素通过 pivot 划分成两部分，
// 使得 pivot 左边的元素都小于它，右边的元素都大于它，然后返回 pivot 的下标
int _partition(vector<int> &nums, int left, int right)
{
  int pivot = nums[left]; // 令 pivot 为左边第一个元素
  while (left < right)
  {
    // 如果右边元素大于 pivot，不管；反之，则让它到左边去
    while (left < right && nums[right] >= pivot)
      right--;
    nums[left] = nums[right];
    // 如果左边元素小于 pivot，不管；反之，则让它到右边去
    while (left < right && nums[left] <= pivot)
      left++;
    nums[right] = nums[left];
  }
  nums[left] = pivot; // 最后记得恢复 pivot！！！
  return left;
}

// 将 nums 通过 _partition 划分成两部分，对每个部分调用 _quick_sort
void _quick_sort(vector<int> &nums, int left, int right)
{
  if (left < right)
  {
    int p = _partition(nums, left, right);
    _quick_sort(nums, left, p - 1);
    _quick_sort(nums, p + 1, right);
  }
}

void QuickSort(vector<int> &nums)
{
  _quick_sort(nums, 0, nums.size() - 1);
}

Procedure 𝐁𝐮𝐜𝐤𝐞𝐭-𝐒𝐨𝐫𝐭

Create $d$ empty lists. (These are the buckets.)
Scan through input, for each item, append it to the end of the corresponding list.
Concatenate all lists.

This algorithm only takes $\Theta(n)$ time.

This is not a comparison based algorithm.
No comparison between items are made.
Instead the algorithm uses actual values of the items.

  
void bucketSort(vector<int> &nums) 
{
    int n = nums.size();
    int mn = nums[0], mx = nums[0];
    for (int i = 1; i < n; i++) 
    {
        mn = min(mn, nums[i]);
        mx = max(mx, nums[i]);
    }
    int size = (mx - mn) / n + 1;   // size 至少要为1
    int cnt = (mx - mn) / size + 1; // 桶的个数至少要为1
    vector<vector<int>> buckets(cnt);
    for (int i = 0; i < n; i++) 
    {
        int idx = (nums[i] - mn) / size;
        buckets[idx].push_back(nums[i]);
    }
    for (int i = 0; i < cnt; i++) 
    {
        sort(buckets[i].begin(), buckets[i].end());
    }
    int index = 0;
    for (int i = 0; i < cnt; i++) 
    {
        for (int j = 0; j < buckets[i].size(); j++) 
        {
            nums[index++] = buckets[i][j];
        }
    }
}

Procedure 𝐑𝐚𝐝𝐢𝐱-𝐒𝐨𝐫𝐭

  
int maxbit(int data[], int n) // 辅助函数，求数据的最大位数
{
    int maxData = data[0]; // 最大数
    // 先求出最大数，再求其位数，这样有原先依次每个数判断其位数，稍微优化点。
    for (int i = 1; i < n; ++i)
    {
        if (maxData < data[i])
            maxData = data[i];
    }
    int d = 1;
    int p = 10;
    while (maxData >= p)
    {
        maxData /= 10;
        ++d;
    }
    return d;
}

void radixsort(int data[], int n) // 基数排序
{
    int d = maxbit(data, n);
    int *tmp = new int[n];
    int *count = new int[10]; // 计数器
    int i, j, k;
    int radix = 1;
    for (i = 1; i <= d; i++) // 进行 d 次排序
    {
        for (j = 0; j < 10; j++)
            count[j] = 0; // 每次分配前清空计数器
        for (j = 0; j < n; j++)
        {
            k = (data[j] / radix) % 10; // 统计每个桶中的记录数
            count[k]++;
        }
        for (j = 1; j < 10; j++)
            count[j] = count[j - 1] + count[j]; // 将 tmp 中的位置依次分配给每个桶
        for (j = n - 1; j >= 0; j--)            // 将所有桶中记录依次收集到 tmp 中
        {
            k = (data[j] / radix) % 10;
            tmp[count[k] - 1] = data[j];
            count[k]--;
        }
        for (j = 0; j < n; j++) // 将临时数组的内容复制到 data 中
            data[j] = tmp[j];
        radix = radix * 10;
    }
    delete[] tmp;
    delete[] count;
}

Summary

Algorithms	Best	Worst	Average	In/Out-Place	Stability
Insertion-Sort	$O(n^2)$	$O(n^2)$	$O(n^2)$	In-place	True
Merge-Sort	$O(n\log{n})$	$O(n\log{n})$	$O(n\log{n})$	Out-place	True
Heap-Sort	$O(n\log{n})$	$O(n\log{n})$	$O(n\log{n})$	In-place	False
Selection-Sort	$O(n^2)$	$O(n^2)$	$O(n^2)$	In-place	False
Shell-Sort	$O(n\log{n})$	$O(n^2)$	-	In-place	False
Bubble-Sort	$O(n)$	$O(n^2)$	$O(n^2)$	In-place	True
Quick-Sort	$O(n\log{n})$	$O(n\log{n})$	$O(n\log{n})$	In-place	False
Bucket-Sort	$O(n + k)$	$O(n^2)$	$O(n + k)$	Out-place	True
Radix-Sort	$O(n \cdot k)$	$O(n \cdot k)$	$O(n \cdot k)$	Out-place	True

All the images in this article are derived from this blog. ↩︎

Schoolwork, Notes

程序算法代码

本文由作者按照 CC BY 4.0 进行授权

Procedure 𝐈𝐧𝐬𝐞𝐫𝐭𝐢𝐨𝐧-𝐒𝐨𝐫𝐭1

Procedure 𝐌𝐞𝐫𝐠𝐞-𝐒𝐨𝐫𝐭

Procedure 𝐇𝐞𝐚𝐩-𝐒𝐨𝐫𝐭

Procedure 𝐒𝐞𝐥𝐞𝐜𝐭𝐢𝐨𝐧-𝐒𝐨𝐫𝐭

Procedure 𝐒𝐡𝐞𝐥𝐥-𝐒𝐨𝐫𝐭

Procedure 𝐁𝐮𝐛𝐛𝐥𝐞-𝐒𝐨𝐫𝐭

Procedure 𝐐𝐮𝐢𝐜𝐤-𝐒𝐨𝐫𝐭

Procedure 𝐁𝐮𝐜𝐤𝐞𝐭-𝐒𝐨𝐫𝐭

Procedure 𝐑𝐚𝐝𝐢𝐱-𝐒𝐨𝐫𝐭

Summary

热门标签

Procedure 𝐈𝐧𝐬𝐞𝐫𝐭𝐢𝐨𝐧-𝐒𝐨𝐫𝐭¹