🧑🏻‍💻 堆（小根堆）

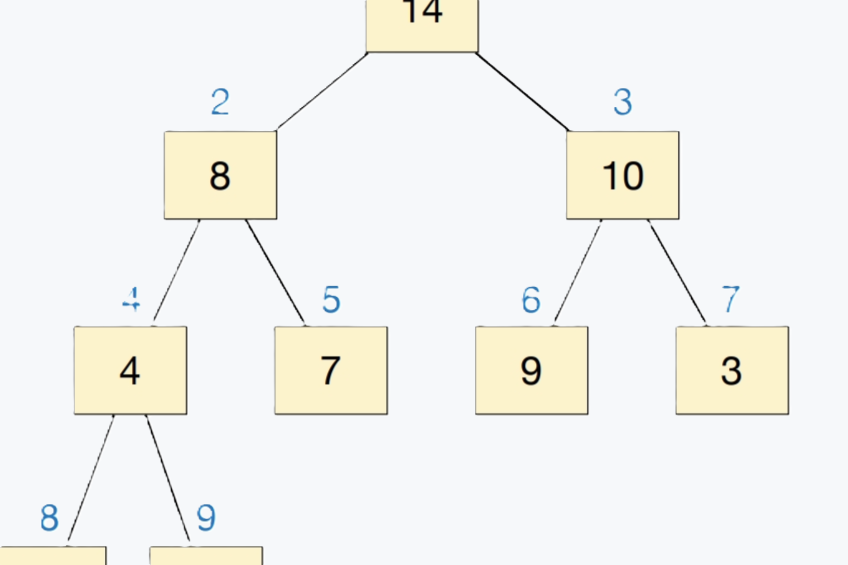
小根堆是一种二叉堆数据结构，其中每个节点的值都小于或等于其子节点的值。以下是实现一个小根堆的 C++ 代码，一共支持六种操作。

• push(x)：将元素 $x$ 插入堆中。
• pop()：删除堆中的最小元素。
• top()：返回堆中的最小元素，但不删除它。
• size()：返回堆中元素的数量。
• decrease(i, k)：将第 $i$ 次 push 操作（其他类型操作不参与编号）插入的元素减少为 $k$，保证 $k$ 小于原值。
• print：打印堆。

#include <bits/stdc++.h>
using namespace std;

class minHeap
{
private:
  vector<int> vec;             // items in the heap
  vector<int> order;           // order of insertion
  int insert_index = 0;

public:
  void push(int x);            // push x into the heap
  void pop();                  // remove the minimum item from the heap
  int top();                   // return the minimum item of the heap
  int size();                  // return number of items in the heap
  void decrease(int i, int k); // reduce the ith-inserted item to k
  void print();                // print the heap
};

void minHeap::push(int x)
{
  // simply put the item to the end of the array
  vec.push_back(x);
  order.push_back(insert_index++);

  // maintain heap property after insertion:
  // along the path to root, compare and swap
  int index = vec.size() - 1;
  while (index > 0 && vec.at(index) < vec.at((index - 1) / 2))
  {
    swap(vec.at(index), vec.at((index - 1) / 2));
    swap(order.at(index), order.at((index - 1) / 2));
    index = (index - 1) / 2;
  }
  return;
}

void minHeap::pop()
{
  if (vec.size() == 1)
  {
    vec.pop_back();
    order.pop_back();
    return;
  }

  // remove the minimum item (root) from the heap,
  // and move the last item to the root
  vec.at(0) = vec.at(vec.size() - 1);
  order.at(0) = order.at(order.size() - 1);
  vec.pop_back();
  order.pop_back();

  int index = 0;
  while (index < vec.size())
  {
    int l_index = 2 * index + 1;
    int r_index = 2 * index + 2;
    int min_index = index;

    // compare with children, swap with the smaller one
    if (l_index < vec.size() && vec.at(l_index) < vec.at(min_index))
      min_index = l_index;
    if (r_index < vec.size() && vec.at(r_index) < vec.at(min_index))
      min_index = r_index;
    if (min_index != index)
    {
      swap(vec.at(index), vec.at(min_index));
      swap(order.at(index), order.at(min_index));
      index = min_index;
    }
    else
      break;
  }
}

int minHeap::top() { return vec.at(0); }

int minHeap::size() { return vec.size(); }

void minHeap::decrease(int i, int k)
{
  // find the ith insertion, reduce it to k
  int i_index = 0;
  for (i_index; i_index < order.size(); i_index++)
  {
    if (order.at(i_index) == i)
      break;
  }
  vec.at(i_index) = k;

  // maintain min-heap property
  while (i_index > 0 && vec[i_index] < vec[(i_index - 1) / 2])
  {
    swap(vec[i_index], vec[(i_index - 1) / 2]);
    swap(order[i_index], order[(i_index - 1) / 2]);
    i_index = (i_index - 1) / 2;
  }
}

void minHeap::print()
{
  for (int i = 0; i < vec.size(); i++)
    cout << vec[i] << " ";
  cout << endl;
}