🧑🏻‍💻 图的遍历

广度优先搜索

• Basic Idea of BFS:
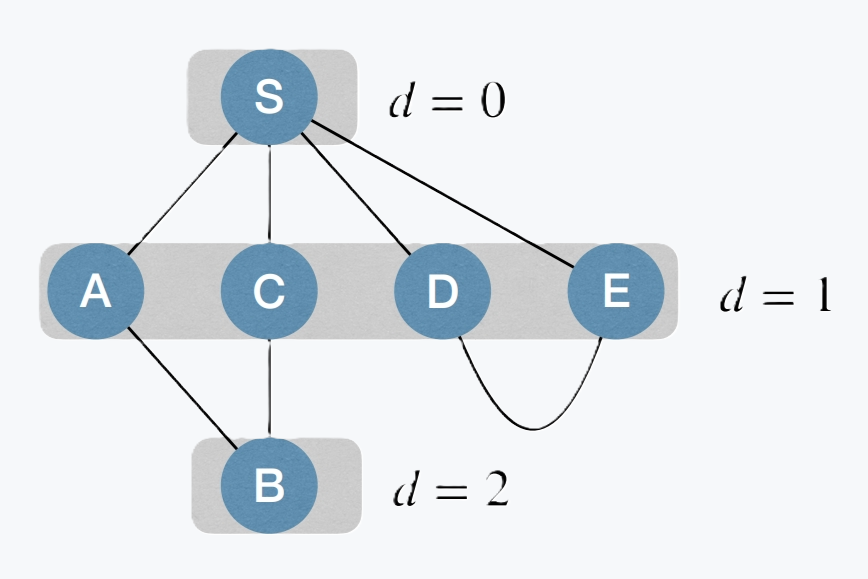
  • Start at the source node $s$;
  • Visit other nodes (reachable from $s$) “layer by layer”
• How to implement BFS?
  • Use a FIFO Queue!
• Nodes have 3 status:
  • Undiscovered: Not in queue yet.
  • Discovered but not visited: In queue but not processed.
  • Visited: Ejected from queue and processed.
• What if the graph is not connected?
  • Easy, do a BFS for each connected component!

BFSSkeleton(G, s):
for each $u$ in $V$
  $u.dist := INF, u.discovered := False,$
  $s.dist := 0, s.discovered := True$
$Q.enque(s)$
while $!Q.empty()$
  $u := Q.dequeue()$
  for each $edge(u, v)$ in $E$
    if $!v.discovered$
      $v.dist := u.dist + 1$
      $v.discovered := True$
      $Q.enque(v)$

---

示例代码：打印一号点到其余每一个点的最短路程。

// Author: Chen Xin
// Date: 2024-11-25

#include <bits/stdc++.h>
using namespace std;

class Graph
{
private:
    int n;
    vector<vector<int>> graph;

public:
    Graph(int verticles);
    void addEdge(int u, int v);
    void findShortest();
};

Graph::Graph(int verticles)
{
    n = verticles;
    graph.resize(verticles);
}

void Graph::addEdge(int u, int v)
{
    graph[u].push_back(v);
    graph[v].push_back(u);
}

void Graph::findShortest()
{
    queue<int> discovered;
    vector<int> distToFirst(n, -1);
    discovered.push(0);
    distToFirst[0] = 0;

    // BFS
    while (!discovered.empty())
    {
        int prev = discovered.front();
        discovered.pop();
        for (int neighbor : graph[prev])
        {
            if (distToFirst[neighbor] == -1)
            {
                distToFirst[neighbor] = distToFirst[prev] + 1;
                discovered.push(neighbor);
            }
        }
    }

    for (int i = 1; i < n; i++)
    {
        if (i < n)
            cout << distToFirst[i] << " ";
        else
            cout << distToFirst[i] << endl;
    }
}

int main()
{
    int N, M, u, v;
    cin >> N >> M;
    Graph graph(N);
    while (M--)
    {
        cin >> u >> v;
        graph.addEdge(u - 1, v - 1);
        // 题中顶点编号为 1 ~ N，实际存储时为 0 ~ (N-1)，故进行转换
    }
    graph.findShortest();
    return 0;
}

深度优先搜索

• Basic Idea of DFS, much like exploring a maze:
  • Use a ball of string and a piece of chalk.
  • Follow path (unwind string and mark at intersections), until stuck (reach dead-end or already-visited place).
  • Backtrack (rewind string), until find unexplored neighbor (intersection with unexplored direction).
  • Repeat above two steps.
• What if the graph is not (strongly) connected?
  • Do DFS from multiple sources.

DFSSkeleton(G, s):
$s.visited := True$
for each $edge(s, v)$ in $E$
  if $!v.visited$
    $DFSSkelecton(G, v)$

DFSIterSkeleton(G, s):
Stack $Q$
$Q.push(s)$
while $!Q.empty()$
  $u := Q.pop()$
  if $!u.visited$
    $u.visited := True$
    for each $edge(u, v)$ in $E$
      $Q.push(v)$

---

示例代码：判断图中是否存在环。

// Author: Chen Xin
// Date: 2024-11-25

#include <bits/stdc++.h>
using namespace std;

#define UNVISITED -1
#define VISITING 0
#define VISITED 1

class Graph
{
private:
    vector<vector<int>> graph;
    int n;

public:
    Graph(int verticles);
    void addEdge(int u, int v);
    bool findCycle();
    bool DFS(int index, vector<int> &isVisited);
};

Graph::Graph(int verticles)
{
    n = verticles;
    graph.resize(verticles);
}

void Graph::addEdge(int u, int v)
{
    graph[u].push_back(v);
}

bool Graph::findCycle()
{
    vector<int> isVisited(n, UNVISITED);
    for (int i = 0; i < n; i++)
    {
        if (isVisited[i] == UNVISITED)
        {
            if (DFS(i, isVisited))
                return true;
        }
    }
    return false;
}

bool Graph::DFS(int index, vector<int> &isVisited)
{
    isVisited[index] = VISITING;
    for (int node : graph[index])
    {
        if (isVisited[node] == UNVISITED)
        {
            if (DFS(node, isVisited))
                return true;
        }
        // 节点正在被访问，说明存在环
        else if (isVisited[node] == VISITING)
            return true;
    }
    isVisited[index] = VISITED;
    return false;
}

int main()
{
    int N, M, u, v;
    cin >> N >> M;
    Graph graph(N);
    while (M--)
    {
        cin >> u >> v;
        graph.addEdge(u - 1, v - 1);
        // 题中顶点编号为 1 ~ N，实际存储时为 0 ~ (N-1)，故进行转换
    }
    cout << (graph.findCycle() ? "YES" : "NO") << endl;
    return 0;
}